Category: Bookkeeping

It’s essential to ensure that the data meets these assumptions to obtain accurate and reliable results. By using an Anova calculator, researchers and data analysts can quickly and easily perform variance analysis and gain valuable insights into their data. In statistics, variance assesses how effectively the mean represents a dataset. Higher variance suggests greater data range, potentially making the mean less representative, unlike in cases of lower variance. You will need the mean of the data set, arithmetic difference, and many additions and subtractions to find variance. In statistics, the variance of a random variable is the mean value of the squared distance from the mean.

Statistical Mean Formula

This tool is useful to calculate sample variance even when analyzing a subset of data, especially when it’s impractical to collect data from an entire population. Sample variance and population variance differ mainly in their data scope and formulas. Population variance, however, includes the squared deviations for the entire population and divides the sum of squared differences by the total number of data points.

In statistics, household employment taxes the average of the squared deviations from the mean is said to be the variance. It decides whether the data values are closer or far from the average value. Population variance is used when analyzing an entire dataset, dividing by n (total number of values).

Using a Variance Calculator: Step by Step Solution

The calculator will automatically recognize and process the numbers, ensuring they are valid for calculations. In simpler terms, if all data in a set are very similar to each other, the variance will be low, indicating little dispersion. Conversely, if the data vary significantly, the variance will be high, signaling greater dispersion. Using the wrong formula can lead to incorrect interpretations, especially in research or financial analysis.

Understanding this helps in making more informed decisions and in evaluating the reliability of data. Variance and standard deviation are fundamental statistical concepts that measure the spread of data points in a dataset. While variance shows how far numbers are from the mean, standard deviation provides a more intuitive measure by representing the dispersion in the same unit as the data. In this equation, σ2 refers to population variance, xi is the data set of population, μ is the mean of the population data set, and N refers to the size of the population data set. It can be disproportionately influenced by outliers, which significantly impact the sum of all the squared differences together. Additionally, variance does not indicate the direction of data spread and can be less intuitive due to the squaring of all the squared differences together.

Step 2: Clicking the Calculate Button

To calculate the variance from a set of values, specify whether the data is for an entire population or from a sample. Values must be numeric and may be separated by commas, spaces or new-line. Population variance is calculated when data for the entire population is available. It is obtained by dividing the sum of the squared differences between each data point and the population mean by the total number of data points in the population (N). This formula does not require correction, as it is based on all available data. Sample variance is calculated when only a sample of the population is available.

The F-statistic and p-value are used to determine the significance of the differences. Use this calculator to compute the variance from a set of numerical values. A small variance indicates the distribution of the random variable close to the mean value. If the variance is greater, it shows that the random variable is far from the average value. In summary, variance allows you to see how data cluster around the mean and whether there is a lot or little variability in the set.

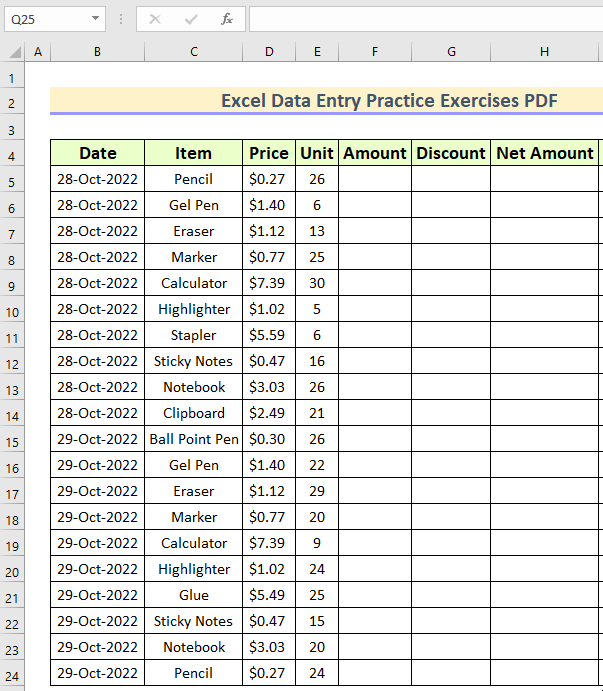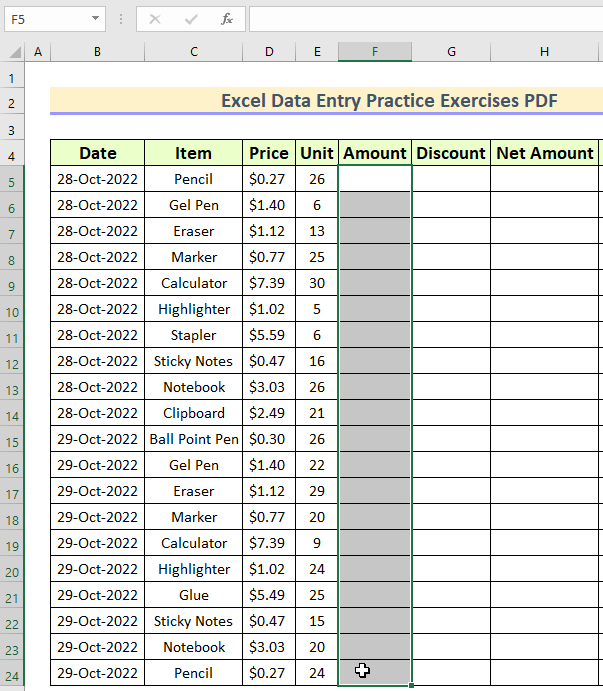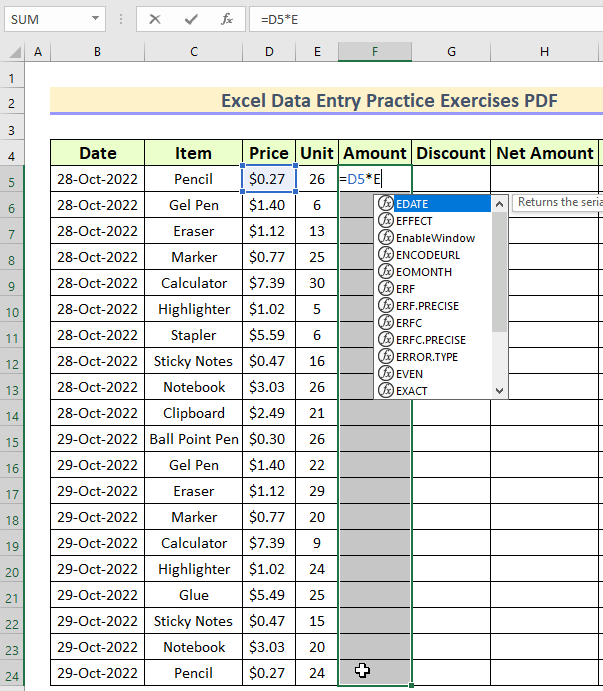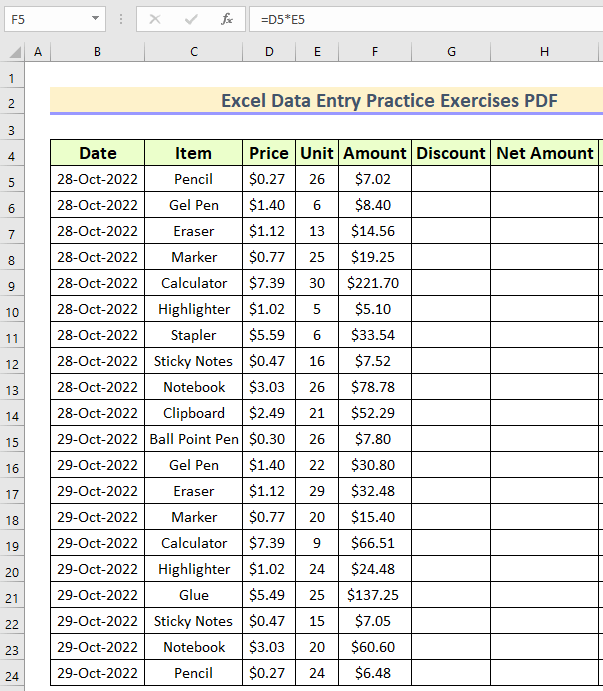
Calculating values from the table:

• Higher variance suggests greater data range, potentially making the mean less representative, unlike in cases of lower variance.
• For an unbiased statistic, we expect to get a standard deviation of 4 and a variance of 16.You may notice that dividing by (n-1) yields better results than dividing by n.
• Sample variance is used when working with a subset of data, dividing by n-1 to account for sampling variability.
• It helps analysts understand data variability, assess risk in finance, and make informed decisions based on data trends.

A population variance and sample variance formula calculator simplifies the process of determining the dispersion of data points in a data set. Whether you need to calculate population variance, sample variance, or both, this tool offers a step-by-step solution, ensuring accuracy and ease. Variance stands as a cornerstone in statistical analysis, offering deep insights into the dispersion and variability of data within a whole set of data. Understanding and accurately calculating variance, both for a sample and an entire population, is essential for making informed decisions based on data. This guide will delve into various aspects of variance calculation, emphasizing the role of a Variance Calculator in simplifying this process. Population variance is calculated using the population variance formula.

Follow these steps to measure the variance for the given data set using this formula. Variance calculator is an online free tool to calculate the variation of each number in a data set from the mean value of that data set. You can use this tool to understand and solve complex and lengthy variance problems. You can solve this problem by using the population variance calculator above or manually. Sample variance uses n-1 in the denominator instead of n to correct for bias when estimating population variance from a sample. This makes sample variance slightly larger than population variance in most cases.

Variance formula

• In statistics, the variance of a random variable is the mean value of the squared distance from the mean.
• Understanding this helps in making more informed decisions and in evaluating the reliability of data.
• The term “population” refers to the entire number of relevant observations.
• Use the variance calculator to compute both sample variance and population variance, complete with a step-by-step solution, and then present the results in APA format.
• Choosing the correct type of variance—population or sample—is crucial for accurate statistical analysis.

You can also use the population variance calculator above to calculate the variance for your set of data. The first example is of population variance and the second example is of sample variance. Variance calculator is used to find the variance of sample and population data. This variance solver also finds the standard deviation, the mean, and the statistical sum of squares in one click. Variance analysis is a crucial aspect of statistical analysis, enabling researchers and data analysts to understand the differences between various groups or datasets. One of the most widely used methods for variance analysis is the Analysis of Variance (ANOVA).

It helps researchers and data analysts to compare the means of two or more groups and determine if there are any significant differences between them. The variance is one of the measures of dispersion, that is a measure of by how much the values in the data set are likely to differ from the mean of the values. Squaring the deviations ensures that negative and positive deviations do not cancel each other out. It represents the average of squared differences between each value and the mean.

This calculator provides the result of the mean, standard deviation, and the sum of squares along with steps. When you do not have data for the entire population, you calculate the sample variance from the sampled data. Unlike population variance, when calculating the sample variance, you divide by (n – 1); in this case, the resulting statistic is unbiased.

Variance is a statistical measure that indicates how much a set of numbers differs from the mean (average) value. It helps determine the spread or dispersion of data points within a dataset. A higher variance means that the numbers are more spread out, while a lower variance indicates that they are closer to the mean. Variance is a statistical measure that quantifies the dispersion or variability of a data set with respect to its statistical mean. Essentially, variance indicates how far individual values are from the average of the data set.

If you are working with a sample, divide the sum of the squares by the total number of data points minus one (n-1) to obtain the sample variance. If you are working with the entire population, divide by the total number of data points (N) to obtain the population variance. Population standard deviation is calculated from the entire population using the population mean, while sample population standard deviation only uses sample data and the sample mean. The formula for each is the square root of their respective variances, aligning the values of the units of measure with those of the data. It represents the square root of the variance, providing a measure of data spread in the same units as the data itself. Variance calculator is used to find the actual distance of the data values from the mean.

A variance calculator is a statistical tool used to calculate the variance of a set of data. It simplifies the process to calculate variance, by automating the computation of squared differences between each data point and the mean. Users input a series of data values, and the variance calculator provides the variance, indicating the degree of spread in the data set. This tool is particularly useful in data analysis, saving time and reducing errors that can occur in manual calculations. A sample variance calculator is a tool designed for calculating the variance of a sample data set. It applies the sample variance formula, considering the sample mean and the sample size.

Specify whether the total number of data points represent a sample population or the entire population. This choice will determine the variance formula used in the calculation. Scroll the above table for more results.Choose the population variance only if you have the data from the entire population, otherwise use the sample variance.

News & World Report, as well as wrote and edited content about education financing and financial literacy for multiple online properties, e-courses and more. Ryan also previously oversaw the production of life science journals as a managing editor for publisher Cell Press. No, it is relatively easy to use, although corrections can be more challenging. However, so if you work with a professional accountant, they will likely have an in-depth understanding of the platform and can guide you through its functions. Currently, the ProAdvisor Preferred Pricing program only supports them as a bundle. When you pay for your client’s subscription, it does not affect the billable user count.

QuickBooks Online can be a more cost-efficient option for businesses with multiple users that don’t want to navigate the steep learning curve of QuickBooks Desktop. However, QuickBooks Desktop may be the better value for businesses that want a locally installed software option with enhanced accounting features. Most integrations come with monthly subscription fees, so be sure to account for these extra costs when calculating your total costs for QBO. QuickBooks Online payroll costs between $50-$130/month plus $6-$11/month per employee.

It offers solid core accounting and operational efficiency features at a moderately competitive price, particularly with the 50% off deal for the first three months. On top of that, it provides the best help and support options in our research, with 24/7 chatbot assistance and regularly available human representatives, even on the weekend. QuickBooks Online is one of the preeminent cloud-based accounting software platforms on the market. With four plans available, there are several options from which to choose, depending on your needs. In this guide, we’ll break down QuickBooks Online pricing, including plans, key features, and alternative platform costs so you can decide which option is best for you. You will have access to the QuickBooks dashboard once you’ve chosen a plan.

QuickBooks Online Plus Pricing

• Securely message clients, share documents, and consolidate notes and contact info from a single dashboard.
• The default categories offered by QuickBooks Online can be altered as necessary.
• However, bookkeepers and accountants are eligible for up to 30% off the subscription price for their clients.
• Ryan also previously oversaw the production of life science journals as a managing editor for publisher Cell Press.

QuickBooks Online is a cloud-based accounting platform while QuickBooks is a desktop program that provides additional inventory management features. FreshBooks is great for self-employed individuals, sole proprietors and independent contractors. It is incredibly user-friendly and easy to navigate, so if you are a sole proprietor looking for basic accounting software, FreshBooks will meet your needs at a relatively low cost. Its basic plan is in line with QuickBooks Simple Start, at $15 per month. We understand the importance of a reliable monthly bill for you and your clients, which is why we are offering the ongoing monthly discount to accounting professionals via the ProAdvisor discount. When you select this option, Intuit will bill your firm each month for all eligible client subscriptions and you can enjoy the ongoing savings month after month.

QuickBooks Online Accountant is free for your firm. Just pay to add clients.

• It also prevents the business owner from understanding the health of their finances, which is the whole point of bookkeeping.
• For a subscription-based Desktop plan, learn more about QuickBooks Desktop Premier Plus.
• The answers to these questions should help you determine which plan is best for your business.
• Solopreneur is less expensive, and Enterprise is typically pricier.

This plan is designed for freelancers who file a Schedule C IRS form to report their income as sole proprietor. Our unbiased reviews and content are supported in part by affiliate partnerships, and we adhere to strict guidelines to preserve editorial integrity. The editorial content on this page is not provided by any of the companies mentioned and has not been reviewed, approved or otherwise endorsed by any of these entities.

QuickBooks Online offers four pricing plans that start at $35/month and cost up to $235/month, depending on the number of features and users your business needs. Intuit created QuickBooks Online, a cloud-based accounting program, to make bookkeeping, financial management, and payroll processing easier for companies. Users may access their financial data from any location with an internet connection because of QuickBooks Online’s flexibility, which sets it apart from the classic desktop version. Startups, small businesses, and even larger enterprises choose it because of its comprehensive capabilities and easy-to-use interface.

Learn how to know which plan is right for you and what additional costs to expect before subscribing to QuickBooks Online. Clarify complexity with efficient inventory management and integrated payroll and time tracking. Plus, with access for up to 40 users, Enterprise can scale with your business as it grows.

QuickBooks Online Advanced

Though QuickBooks Online has a learning curve, it balances out with all the readily available resources to learn and navigate the program. To increase profits, you must maximize your tax deductions, which QuickBooks Online can help you do with its tax deduction tools. With the “snap and store” feature, your receipts are immediately entered. The software can keep track of your miles for business-related trip expense deductions.

Whether your client is a new business or a seasoned entrepreneur — there’s a QuickBooks for them

By providing feedback on how we can improve, you can earn gift cards and get early access to new features. If you want to give QuickBooks a try before buying, you can sign up for a free 30-day trial or use the company’s interactive test drive that’s set up with a sample company. QuickBooks Online plans are incredibly scalable, so you can start small and upgrade to a larger plan in the future.

Those with QuickBooks Online accounts are potentially eligible, though they’ll still need to qualify on the strength of their accounting history. For a one-time fee (which is no longer publicly listed online, as of January 2025, but used to cost $50), QuickBooks Live Bookkeeping will set you up with an expert for one session. Reporting tools are available on the Simple Start plan but they are a bit limited. Vehicle tracking is included, too, should you need to invoice for fuel and driving time for any job. You can create an unlimited number of invoices and estimates, track your expenses and manage up to 1,099 contractors. You can bring live bank feeds qbo accountant pricing into your account and access a range of third-party integrations.

This service gives you access to a QuickBooks debit card, cash flow forecasting, and QuickBooks Envelopes, which is a place to set aside savings. Learn more about the details of each additional QuickBooks fee below. Here’s a complete breakdown of what’s included with each QuickBooks Online pricing plan.

You don’t have to sacrifice your day to clean up your clients’ books. Custom bank feeds get rid of tedious data entry by downloading, categorizing, and updating transactions automatically in QuickBooks. QuickBooks Solopreneur is a “lite” version of the online product. It’s ideal for people who earn income from a variety of sources and helps to separate personal and business finances.

With the ProAdvisor discount, you receive our best long-term savings option for clients new to QuickBooks, including our only ongoing discount. To maintain flexibility, the ProAdvisor Preferred Pricing program has two options for monthly billing. QBO also won’t teach you accounting and business principles or provide monthly checklists on how to run your bookkeeping business efficiently.

Simple Start is the minimum required plan to use for professional bookkeeping. This plan costs $30 monthly, although you can get 50% off for the first three months. QuickBooks Online is a subscription-based product that gives you the freedom to work on the go. You can access and sync data across all your devices – computer, tablet and smartphone. Your data is securely backed up and you have instant access to the latest product and feature updates. Additionally, you can connect QuickBooks Online to over 300 apps you already use, and save even more time.

Their mobile app for iOS and Android devices ensures you get all the essential capabilities that QuickBooks Online provides. Granted, the right plan for you will vary depending on your needs, and there are alternative accounting software options on the market that may also be a good fit. Still, QuickBooks Online offers an unbeatable range of features, packaged in a solid interface with good support. That’s why at Tech.co, we have full-time product researchers to re-run this testing process regularly. It’s the only way to ensure our results remain reflective of the present day.

At a contribution margin ratio of \(80\%\), approximately \(\$0.80\) of each sales dollar generated by the sale of a Blue Jay Model is available to cover fixed expenses and contribute to profit. The contribution margin ratio for the birdbath implies that, for every \(\$1\) generated by the sale of a Blue Jay Model, they have \(\$0.80\) that contributes to fixed costs and profit. Thus, \(20\%\) of each sales dollar represents the variable cost of the item and \(80\%\) of the sales dollar is margin. Just as each product or service has its own contribution margin on a per unit basis, each has a unique contribution margin ratio. Cost volume profit (CVP) analysis is a managerial accounting technique used to determine how changes in sales volume, variable costs, fixed costs, and/or selling price per unit affect a business’s operating income. The focus may be on a single product or on a sales mix of two or more different products.

Some other helpful tools for business

For managerial use, a proper contribution margin income statement is prepared to compute this figure. A contribution margin analysis can be done for an entire company, single departments, a product line, or even a single unit by following a simple formula. The contribution margin can be presented in dollars or as a percentage. Alternatively, the company can also try finding ways to improve revenues. However, this strategy could ultimately backfire and hurt profits if customers are unwilling to pay the higher price.

Contribution margin vs. gross margin

Contribution margin ratio is equal to contribution margin divided by sales. In this example, if we had been given the fixed expenses, we could also find out the firm’s net profit. Below is a break down of subject weightings in the FMVA® financial analyst program. As you can see there is a heavy focus on financial modeling, finance, Excel, business valuation, budgeting/forecasting, PowerPoint presentations, accounting and business strategy. Here, we are calculating the contribution margin on a per-unit basis, but the same values would be obtained if we had used the total figures instead. The 60% CM ratio implies the contribution margin for each dollar of revenue generated is $0.60.

Weighted average contribution margin ratio equals the sum of contribution margins of all products divided by total sales. It helps investors assess the potential of the company to earn profit and the part of the revenue earned that can help in covering the fixed cost of production. The business can interpret how the sales figures are affecting the overall profits.

Regardless of how much it is used and how many units are sold, its cost remains the same. However, these fixed costs become a smaller percentage of each unit’s cost as the number of units sold increases. To calculate the contribution margin, we must deduct the variable cost per unit from the price per unit.

Strategies to Reduce Inventory Holding Costs in 2024

Only when 590 smoothies are sold does something remain from the contribution margin, so that a profit is then made. In conjunction with the break-even analysis, we can now also calculate how many smoothies the company needs to sell to cover its fixed costs. The fixed costs total £1,000 per month for rent, running costs of the smoothie production line and salaries for the staff. Contribution margin is a key figure that indicates what proportion of revenue remains after variable costs have been deducted. The remaining amount must at least cover the company’s fixed costs so that no losses are incurred.

What is Unit Contribution Margin?

• To find the contribution margin, subtract the total variable costs from the total sales revenue.
• If the fixed costs remained constant, the selling price could be reduced to $8 and still cover the variable and fixed costs.
• Find out what a contribution margin is, why it is important, and how to calculate it.
• Buying items such as machinery is a typical example of a fixed cost, specifically a one-time fixed cost.

To make a product profitable, the remaining income after variable costs must be more than the company’s fixed costs, such as insurance and salaries. Variable costs are not typically reported on general purpose financial statements as a separate category. Thus, you will need to scan the income statement for variable costs and tally the list. Some companies do issue contribution margin income statements that split variable and fixed costs, but this isn’t common. The contribution margin formula is calculated by subtracting total variable costs from net sales revenue. The contribution margin per unit formula is calculated by subtracting the variable costs per unit from the selling price per unit.

You’ll often turn to profit margin to determine the worth of your business. It’s an important metric that compares a company’s overall profit to its sales. However, if you want to know how much each product contributes to your bottom line after covering its variable costs, what how to obtain a copy of your tax return you need is a contribution margin. Weighted average contribution margin per unit equals the sum of contribution margins of all products divided by total units.

We will discuss how to use the concepts of fixed and variable costs and their relationship to profit to determine the sales needed to break even or to reach a desired profit. You will also learn how to plan for changes in selling price or costs, whether a single product, multiple products, or services are involved. If you need to estimate how much of your business’s revenues will be available to cover the fixed expenses after dealing with the variable costs, this calculator is the perfect tool for you. You can use it to learn how to calculate contribution margin, provided you know the selling price per unit, the variable cost per unit, and the number of units you produce. The calculator will not only calculate the margin itself but will also return the contribution margin ratio. Contribution margin income statement, the output of the variable costing is useful in making cost-volume-profit decisions.

The contribution margin is a measurement through which we understand how much a company’s net sales will contribute to the fixed expenses and the net profit after covering the variable expenses. So, we deduct the total variable expenses from the net sales while calculating the contribution. Contribution margin is the amount by which an item contributes towards covering fixed costs and profitability of the business.

Fixed costs are production costs that remain the same as production efforts increase. In this example, product A (toy slimes) has a higher sales revenue and volume of units sold but has a lower contribution margin. Whereas product B (animal plushies) has lower sales revenue and volume of units sold, it has a higher contribution margin. Contribution margin ratio equals contribution margin per unit as a percentage of price or total contribution margin TCM expressed as a percentage of sales S. Decisions can be taken regarding new product launch or to discontinue the production and sale of goods that are no longer profitable or has lost its importance in the market. The fixed costs of $10 million are not included in the formula, however, it is important to make sure the CM dollars are greater than the fixed costs, otherwise, the company is not profitable.

• In addition, although fixed costs are riskier because they exist regardless of the sales level, once those fixed costs are met, profits grow.
• Let’s take another contribution margin example and say that a firm’s fixed expenses are $100,000.
• If the contribution margin for an ink pen is higher than that of a ball pen, the former will be given production preference owing to its higher profitability potential.
• The contribution margin (CM) is the profit generated once variable costs have been deducted from revenue.
• It is important to note that this unit contribution margin can be calculated either in dollars or as a percentage.

In addition, whatever is left over after all fixed costs have been covered is profit, so contribution margin also contributes to profit—specifically, what we call operating income. The toy slime has a higher input cost, lowering its contribution margin per unit. This example shows that products with higher sales revenue can give a false sense of profitability, and businesses should be careful of this trap. It’s always a good idea to know your unit contribution margins if you have multiple products. You made $1,000 in total sales revenue after selling 100 units of strawberry bonbons at a $10 selling price per unit.

An important point to be noted here is that fixed costs are not considered while evaluating the contribution margin per unit. As a result, there will be a negative contribution to the contribution margin per unit from the fixed costs component. Knowing how to calculate the contribution margin is an invaluable skill for managers, as using it allows for the easy computation of break-evens and target income sales. This, in turn, can help people make better decisions regarding product & service pricing, product lines, and sales commissions or bonuses.

If they send one to eight participants, the fixed cost for the van would be \(\$200\). If they send nine to sixteen students, the fixed cost would be \(\$400\) because they will need two vans. We would consider the relevant range to be between one and eight passengers, and the fixed cost in this range would be \(\$200\). If they exceed the initial relevant range, the fixed costs would increase to \(\$400\) for nine to sixteen passengers.

After almost a decade of experience in public accounting, he created MyAccountingCourse.com to help people learn accounting & finance, pass the CPA exam, and start their career. Managerial accountants also use the contribution margin ratio to calculate break-even points in the break-even analysis. Suppose you are doing a multi-product production for toy slimes and animal plushies. To illustrate the concepts of contribution margin, consider the following example.

Contribution Margin: What it is and How to Calculate it

The contribution margin is the leftover revenue after variable costs have been covered and it is used to contribute to fixed costs. If the fixed costs have also been paid, the remaining revenue is profit. Overall, per unit contribution margin provides valuable information when used with other parameters in making major business decisions. In accounting, contribution margin is the difference between the revenue and the variable costs of a product. It represents how much money can be generated by each unit of a product after deducting the variable costs and, as a consequence, allows for an estimation of the profitability of a product.

You can even calculate the contribution margin ratio, which expresses the contribution margin as a percentage of your revenue. One can relate the contribution margin to the unit basis as well as to the turnover one makes with the sale of a certain product during a certain period of time. A unit contribution margin is a straightforward way to assess if your product can cover production expenses. You need to work out the contribution margin per unit, the increase in profit if there is a one unit increase in sales.

For example, if a company has received services but has not yet paid for them, the company would record a deferred expense entry. Maintain thorough documentation for all adjusting entries, including the reason for the adjustment, supporting calculations, and any relevant references to accounting standards. This documentation is essential for audits and provides transparency in financial reporting. Perform regular reviews of financial transactions to identify any discrepancies or omissions that may require adjusting entries. A systematic review helps catch errors and ensures that all relevant adjustments are made promptly. By making these adjustments, companies can ensure that their financial statements are accurate and reliable, which is important for making business decisions and meeting regulatory requirements.

Adjusting entries are required to accurately reflect the interest expense for the accounting period. Prepayments and accruals are important concepts in bookkeeping that help ensure accurate financial reporting. Prepaid expenses are costs that have been paid in advance, but are not yet incurred. On the other hand, accrued expenses are costs that have been incurred but not yet paid. Adjusting entries are an essential part of bookkeeping that ensures the accuracy of financial statements. These entries are made at the end of an accounting period to update accounts and reflect accurate financial information.

Ramp helps you maintain clean, traceable adjusting entries by attaching supporting documents and notes to each transaction automatically. Every adjustment has a built-in audit trail, so when you need to explain an entry, the documentation is already there. That makes audit prep faster and builds confidence in your reports year-round. Mistimed or missing adjustments distort profit, inflate assets, and leave gaps in compliance. Companies that maintain timely, well-documented adjustments are able to close their books much faster.

Accrued Expense

• Adjusted journal entries exist because your day-to-day bookkeeping does not always align with when revenue is earned or costs are actually used.
• As your business grows, consider how SolveXia can help modernize your financial processes, reducing manual effort, minimizing errors, and providing better visibility into your accounting operations.
• Some business transactions affect the revenues and expenses of more than one accounting period.
• If you do your own accounting and you use the cash basis system, you likely won’t need to make adjusting entries.

Depreciation refers to the decrease in value of a tangible asset over time due to wear and tear, while amortization refers to the decrease in value of an intangible asset over time. While adjusting entries are commonly made at the end of an accounting period, they can also be made in the middle of a period if needed. Understanding adjustment entries is critical for anyone involved in accounting, finance, or business operations. There are several types of adjustment entries, including accruals, deferrals, estimates, and reclassifications. For example, at the end of the month, a company may have earned $1,000 in interest income on November 28th that has not been received.

What are the 4 types of adjustments in accounting?

This typically happens when you provide services or deliver goods to customers but haven’t billed them by the end of the accounting period. Most critically, these entries reflect the true financial health of your business at period-end. Adjusted journal entries exist because your day-to-day bookkeeping does not always align with when revenue is earned or costs are actually used. Without adjusting entries, your reports would only reflect cash movement and not the financial reality behind it. Misapplication of depreciation and amortization methods can also lead to significant errors.

This involves analyzing the transactions and account balances, calculating the necessary adjustments, and entering the adjustments into the accounting system. The three things to always consider in adjusting entries are the account balances, the financial statements, and the accounting equation. Adjusting entries must ensure top-down and bottom-up planning as an important aspect in epm that the account balances are accurate, the financial statements are complete and correct, and the accounting equation is in balance.

If the trial balance is not in balance, adjusting entries are made to correct the errors. Adjusting entries and regular journal entries differ primarily in their timing and purpose. Regular journal entries are made throughout the accounting period to record day-to-day business transactions, such as sales, purchases, expenses, and cash receipts. These entries ensure that all financial activities are accurately captured and classified in the general ledger.

However, timing the recording of transactions is a challenge for accountants since they need to determine which accounting period should some income and expense items be reported. This is why this assumption also requires an understanding of the accrual principle. Adjusting entries directly affect the balance sheet, which summarizes a company’s assets, liabilities, and equity at a specific point in time. These entries can modify the value of assets and liabilities to reflect their true amounts.

Free Up Time and Reduce Errors

Modern accounting automation tools are changing this landscape by streamlining these critical tasks. To ensure accurate and effective adjusting entries, businesses should follow several best practices. Applying adjusting entries inconsistently from one period to another creates irregularities in financial reporting and makes trend analysis difficult. Understanding adjusting entries becomes clearer when you see them applied to real business situations. Below are practical examples from various industries showing how adjusting entries work in everyday accounting scenarios.

Accrued Revenues

• Unless the interest is paid up to date, the company will always owe some interest to the lender.
• Similarly, if an expense has been incurred but not yet paid, such as rent, the bookkeeper must record an accrued expense by debiting the expense account and crediting the accrued expense account.
• Adjustment entries can also impact a business’s profitability by affecting the amount of revenue and expenses that are recorded in a particular accounting period.
• Regular journal entries are made throughout the accounting period to record day-to-day business transactions, such as sales, purchases, expenses, and cash receipts.
• Uncollected revenue is revenue that is earned during a period but not collected during that period.

Adjustment entries are an important part of the accounting period and the accounting cycle. The accounting period is the period of time for which financial statements are prepared, usually one year. The accounting cycle is the process of recording, classifying, and summarizing financial transactions for a given accounting period.

These two methods differ mainly at the point in time at which income and expense is recognized and recorded. When considering the application of adjusting entries in bookkeeping, it’s crucial to understand the tools and methods used. This plays a pivotal role in ensuring financial statements are accurate and compliant with accounting principles. When recording adjusting journal entries, accountants create a bridge between the day-to-day financial activities recorded in the journal and the financial statements.

Why is it necessary to record adjusting entries in financial statements?

As an asset account, the debit balance of $25,000 will carry over to the next accounting year. To determine if the balance in this account is accurate the accountant might review the detailed listing of customers who have not paid their invoices for goods or services. Let’s assume the review indicates that the preliminary balance in Accounts Receivable of $4,600 is accurate as far as the amounts that have been billed and not yet paid. When it comes to adjusting entries, accounting software makes it easier to make changes. For example, if a business forgot to record an expense in a previous period, they can easily adjust the entry in the software.

Automation eliminates the need for spreadsheets and manual calculations by identifying accounts needing matching funds requirement example adjustment and creating journal entries automatically. This transforms the month-end close process from days to hours, freeing your accounting team to focus on analysis rather than data entry. Even experienced accountants can make errors when handling adjusting entries. Being aware of these common pitfalls can help you maintain more accurate financial records and avoid costly mistakes. Adjusting journal entries shapes the accuracy of every financial report you produce. When your entries reflect earned revenue, used expenses, and updated asset values, your numbers hold up under scrutiny.

Prepaid insurance and prepaid insurance premiums are examples of prepaid expenses, while insurance expense is an example of an accrued expense. Unearned revenues, such as advance payments from customers, should be recognized as liabilities until the revenue is earned. This is important to ensure accurate financial reporting and avoid overstating revenue. In bookkeeping, revenue and expense recognition is an important aspect of financial reporting. The revenue recognition principle states that revenue should be recognized when it is earned, regardless of when payment is received.

Only expenses that are incurred are recorded, the rest are booked as prepaid expenses. Depreciation is the process of statement of retained earnings definition allocating the cost of a tangible fixed asset over its useful life. This type of adjusting entry ensures that the expense of using the asset is matched with the revenue it generates over time.

It is one of the similarities between sales returns and allowances. To close Sales, it must be debited with a corresponding credit to the income summary. Sales Discounts and Sales Returns and Allowances are both contra revenue accounts so each has a normal debit balance.

FAQs on Temporary Accounts

Companies must also present the sales returns and allowances figures in the financial statements. Usually, these are a part of the net sales calculation in the notes to the financial statements. Companies that sell physical goods may also offer sales returns policies. Usually, these companies produce the goods or acquire them from an external source.

Temporary Accounts: Definition and Examples Explained in Detail

This will also help clear the inventory faster than under normal circumstances. The inventory account’s balance is never reset at the conclusion of the accounting month because it is a permanent account. If the return or allowance involves a refund of the customer’s payment, “Cash” is credited. Or, a payable account is credited if the refund is to be made at a future date. When only “Net Sales” is presented in the income statement, its computation is shown in notes to is sales returns and allowances a temporary account financial statements.

How To Record?

For example, ABC company was able to make $500,000 sales in 2020. If the sales account was not closed, it will be carried over to the next accounting period. If the 2020 account was not closed, the balance that would appear at the end of 2021 would be $1,100,000.

Is interest income a temporary account?

Some companies may not have any costs that will require a net sales calculation but many companies do. Sales returns, allowances, and discounts are the three main costs that can affect net sales. Merchandise may need to be returned to the seller for a variety of reasons.

The balances of permanent accounts, on the other hand, are carried forward for each accounting cycle. It is by crossing the income and expenses that the summary is obtained, which is eventually allocated to this account. Subsequently, it can derive from other types of income, such as profit and loss accounts.

• Similarly, the credit side for the entries will depend on how companies compensate their customers.
• The balances of permanent accounts, on the other hand, are carried forward for each accounting cycle.
• The same debit and credit entries are made when allowances are granted to customers for defective merchandise that the customer keeps.
• It is deducted from “Sales” (or “Gross Sales”) in the income statement.
• However, some customers found problems with their lamps and returned them.
• Like sales returns, companies have to record sales allowances separately.

Is Accounts Payable a Temporary Account?

Closing entries are used in accounting to transfer the results of business operations, originally accounted for in temporary revenue and expense accounts, into permanent equity accounts. Processing of closing entries occurs after the end of the company’s accounting period. First, the revenue accounts are closed to the income summary account.

This is usually the case where customers return goods due to they are damaged or defective. In this circumstance, the sales returns and allowances and related accounts are recorded the same as above journal entry. Whenever cash is received, the asset account Cash is debited and another account will need to be credited. Since the service was performed at the same time as the cash was received, the revenue account Service Revenues is credited, thus increasing its account balance. Except for trade discounts — which are not recorded in the financial statements, these discounts appear as a credit on the income statement in the Profit and Loss Account.

These features differentiate sales allowances from sales returns. However, it still affects a company’s revenues in its financial statements. However, companies offer sales allowances before the customer pays for them. Instead, they keep those goods while also receiving a reduction in price for them.

These revenues may arise from the sale of either goods or services. Regardless of their source, revenues play a significant role in a company’s profits and success. Therefore, companies strive to increase the numbers as high as possible.

• All income statement accounts with debit balances are credited to bring them to zero.
• For example, ABC company was able to make $500,000 sales in 2020.
• Cost of Goods Sold has a normal debit balance because it is an expense.
• This is because the sales return and allowances result in a reduction in the cost of goods sold and an increase in merchandise inventory.
• When a company sells a product or service to a customer, it will use the journal entries below.
• Recording sales returns and allowance is straightforward after knowing their accounting treatment.

Before understanding how to record sales returns and allowances, it is crucial to define what these are. Since expenses are usually increasing, think “debit” when expenses are incurred. Debit the accounts receivable account in a journal entry in your records by the full invoice amount of a sale before a cash discount. Credit the sales revenue account by the same amount in the same journal entry.

Accounting for Sales Return

The account contains deductions from purchases for items returned to suppliers, as well as deductions allowed by suppliers for goods that are not returned. He also needs to debit accounts payable to reduce the amount owed the supplier by the amount that was returned. Debit the appropriate tax liability account by the taxes collected on the original sale. Credit cash or accounts receivable by the full amount of the original sales transaction. Companies do not record this transaction as it does not affect the sales or sales return.

The contra revenue account has a debit balance since it is subtracted from the sales revenue account. It is deducted from “Sales” (or “Gross Sales”) in the income statement. On the income statement, the purchases returns and allowances account is subtracted from purchases.

However, after the financial statements for the year are prepared the current year net income and draws will be transferred to this account. Accrued expense is the liability often used for advertising expense (accounts payable is also used). B. Accumulated depreciation is always recorded how much can you contribute to a traditional ira for 2019 as a credit when depreciation expense is incurred (debit). Depreciation expense is recorded when a long term asset is used. Depreciation expense is not paid since the cash was paid when the long-term asset was purchased. Supplies is a current asset and does not depreciate, they are used.

Introduction to Accounting

• The beginning balance of cash and common stock is $50,000 each.
• Paid $7,000 cash and agreed to pay the balance in 6 months.
• The three golden rules of journalizing are based on the nature of the account, i.e., Personal Account, Real Account, or Nominal Account.
• We will provide you with 20 frequently asked journal entry examples on Google along with their logic.
• Exercise D For each of the following unrelated transactions, give the journal entry to record the transaction.

‘Debit all the expenses and losses and Credit all the incomes and gains. The three golden rules of journalizing are based on the nature of the account, i.e., Personal Account, Real Account, or Nominal Account. Seek information on the advantages and disadvantages of working for a CPA firm. Also, inquire about the nature of the work and the training programs offered by the firm for new employees.

Journal Entries

Use the letter of the transaction in place of the date. Account balances are the amounts on the income statement and balance sheet below. Account balances will be the amounts on the income statement and balance sheet below. 1)  Purchased equipment paying $4,000 cash and financing $10,000 to be repaid in monthly payments for 8 months. When following double-entry bookkeeping there needs to be at least 1 debit & 1 credit. The below image is helpful to understand the format of a journal entry.

Journal Entry for Discount Received

Prepare a corrected trial balance as of 2010 December 31. Also, write a description of the effect(s) of each error. The balance of $ 12,000 in the Advertising Expense account was entered as $ 1,200 in the trial balance.

Assets increase with a debit, so accumulated depreciation is increased with a credit (opposite). The amount of insurance that was incurred/used up/expired during the period of time appearing in the heading of the income statement. The amount of insurance premiums that have not yet expired should be reported in the current asset account Prepaid Insurance. Record journal entries for the following transactions. B. Accounts receivable represents what the customer owes the company and is an asset. Assets are credited when they are decreased.

Journal Entry Questions and Solutions

Example – Max Withdrew 1,000 in cash for personal use from his business. Drawings are personal withdrawals made by the owner and act as a reduction in the owner’s capital. Example – Max started a business with 10,000 in cash.

Not yet received is a receivable which is an asset. A related account is Supplies Expense, which appears on the income statement. 20 Collected cash of $ 4,500 from customers on account (see March 12 entry). Asset and expense accounts will have a debit balance.

Determine the balance for each account.C. D. Purchasing an asset is an increase in the asset (debit). Paying cash is a decrease to the asset (credit). Paying later is an increase to a liability (credit). Total debits must always equal total debits.

These methods require little setup and can provide immediate payouts after completing tasks. Simply sell the cards you already own and compare offers online to get the best deal. Most sellers can start earning within a few days, depending on the platform and the demand for the gift cards. Earnings vary depending on the quantity and quality of items sold. Part-time sellers often make $500/month, while dedicated sellers with a curated inventory can earn $20,000/month. A membership website is a great way to build a steady online business if you’re an expert in your field with a knack for creating content.

Your strategy also plays a role – holding domains longer can lead to higher profits. Invest in a good camera, lenses, and editing software to enhance photo quality. Mastering photography skills like composition, lighting, and editing helps make your photos stand out.

Ozon selling features

MyDeal is an Australia-based online marketplace that boasts over a million products in 3,500 different categories. This online marketplace is a great option for those who cannot afford listing charges. Setting up your shop is extremely easy, and you only pay if you make a sale.

Facebook Marketplace is one of the best places to sell online because it exposes you to its 3 billion monthly active users. Depop is an online fashion marketplace with a thriving global community. It’s a place where individuals can buy and sell clothes in a sustainable, inclusive fashion (pun intended). You won’t have to pay listing fees, but you will have to pay $54 monthly maintenance fees for up to 50 product listings. There’s also an additional 6.7% transaction fee per order up to $250. Whether you’re a small start-up looking to build your business or you’re an established seller looking to expand, online marketplaces are great platforms to sell on.

I Tried 4 Popular Non-Aerosol Dry Shampoos, And Here Are My Thoughts

Facebook Marketplace is a great place to list large items that you want to sell locally, such as furniture. The Mercado Libre Cross Border Trade program makes it easy to offer your products to individuals in Mexico, Argentina, Brazil, and Chile. Linio charges a commission fee of 7-15% on every completed order. If you don’t want to handle the shipping and storage duties, you can use Tokopedia’s fulfillment service, TokoCabang. And, with 80 million active users, this selling site is one to consider using.

Products like homewares, furniture, and other large products are significantly prominent on MyDeal. So, if that’s the type of product you’re looking to sell, then it’s a great option for you. It provides professional account management, help with product photoshoots, assistance in cataloging, and more. It also provides a dedicated fulfillment service, making selling logistics streamlined and efficient. Rakuten charges a registration fee, system commission, monthly fee, and other charges to allow online sellers to start operations. To sell on Rakuten, your business needs to be registered in Japan or the US.

Amazon fees

Shopify is the easiest way to create your own store, thanks to more than 200 pre-built website templates. Every store comes with a checkout, SSL security certifications, and beginner-friendly marketing tools. My next move is to take and post new photos, and eventually lower the price.

Handshake is a wholesale and retail marketplace that is owned and run by ecommerce powerhouse, Shopify. The platform allows merchants to sell unique items to both retailers and wholesalers, be they an online store or a brick-and-mortar store. If your total sale exceeds $500, you’ll pay an additional 1.5% flat rate on the amount that exceeds $500. So if you’re looking to avoid listing fees and spending money without first making some back, Bonanza is for you.

It’s free to list and Meta takes no fees, but there are guidelines you need to follow to sell on the platform. Unlike some of the other marketplaces on this list, Decluttr buys your electronics directly. Using their app, scan the barcode of the items you wish to sell for a quote. Decluttr handles all shipping costs and pays for your items as soon as they’re received. You’ll be charged a $0.20 listing fee for each item you sell on Etsy.

That means 70 – 80% of your selling price comes back to you in profit. You can also create a members-only area as part of your online store or even post your menu or bouquet of services if you’re in the hospitality industry. Squarespace pricing for business ranges from $18 to $40 per month. Squarespace also offers multiple payment gateways with minimal charges apart from the card processing fee. You’ll not need to purchase hosting with Squarespace as it’s a hosted platform, so all you’ll need is to register your custom domain.

It’s the best car-selling site if you’re looking to sell your car as soon as possible and make as much profit as possible. Selling goods via the internet can be an incredibly lucrative business model, with the ecommerce space seeing massive growth in the past few years. One of the biggest reasons for this upsurge is that customers find it extremely convenient to buy things from the comfort of their couch without going outside. Founded in 2015, Pinduoduo is one of the fastest-growing eCommerce platforms in the Chinese market. This platform operates primarily as a mobile-centric marketplace. As a seller, you can check out the profiles and reviews of buyers before meeting them.

• Here are some pros and cons of selling products online with Etsy.
• And, certain sites are better for one type of product over another.
• It automatically sends messages to users and can add them as friends.
• Join tens of thousands of ecommerce brands to get more articles like this and our latest resources delivered to your inbox.

This portal is designed for larger inventories, gives performance reports, and has ads packages and listing fee structures. Craigslist is one of the first online marketplaces to exist and is pretty much the bare bones of online selling. It’s fairly straightforward as far as usability goes, but while it’s simple to use, it lacks visual appeal. Faire is an online wholesale marketplace that connects small business owners and independent brands with wholesale product suppliers.

Once your account is set up, upload your product listings with detailed descriptions and quality images. Be sure to set competitive prices to attract Wish’s price-conscious shoppers. No matter what you’re selling or aiming for, there’s an ideal sales channel out there for you. Below, you’ll find our list of the best online selling sites for global merchants. Plus, as an extra tip, we’ll share the perks of having your own store.

• If you think starting your own eCommerce store is out of your depth, you can try some other ways to sell stuff online.
• You can either manage this yourself or partner with an external logistics company to get your products to buyers.
• They built their extremely strong reputation through getting rid of scammers and trolls.
• Shipping costs and methods can make or break your conversion rates and the total number of sales.

Return and Refund Options for Buyers

However, the platform will take 5% of the overall shipping costs should you decide to charge customers a separate shipping fee. Unlike eBay, Etsy is for new products and creations, so don’t join it thinking you’ll be able to sell those old clothes you’ve been wanting to get rid of. Like eBay, Etsy has listing and selling fees, as well as payment processing fees. They also collect fees for taxes for U.S. based sellers, so that is another factor to consider.

Best global online selling sites

Plus, this is a reputable and frequently used site for buyers in Japan. Etsy is a prime online marketplace to use if you sell vintage or handmade products. Meta has also partnered with platforms like Shopify to let merchants list their online marketplace to sell items and find new customers for their business. Facebook Marketplace from Meta is an online selling site where individual people can discover, buy, and sell items on Facebook. If you have design-oriented furniture or home decor to sell online, this is a relevant online selling site. Below are answers to the most commonly asked questions about the best online marketplaces.

If you want to become a Lowe’s registered supplier, you’ll have to first fill out a registration form. There are specific requirements in terms of your insurance levels, compliance with Lowe’s code of conduct, and more. It’s a bit of a cumbersome process and there’s no guarantee you’ll get selected.

Mercado Libre is a leading online marketplace in Latin America, being present in 18 countries spanning from Argentina to Venezuela. But the 4 strongest markets of this marketplace are Brazil, Mexico, Argentina, and Colombia. Another advantage of selling on Etsy is the platform’s simple and user-friendly interface. With just a few steps, your Etsy shop is ready to go live and start selling.

To keep accurate records, you check if total debits match total credits. Profitability and customer satisfaction are two sides of the same coin in modern business. While cutting costs might seem like a straightforward way to increase profits, a more sustainable and impactful approach lies in prioritizing customer satisfaction. The ever-growing demand for efficient supply chains is shaping our world. From coast to coast, Canada’s economy thrives on the smooth flow of goods. Supply chain management (SCM) professionals are the masterminds behind this intricate dance, ensuring everything arrives on time and within budget.

From calculating liabilities to filing returns, we ensure that your business complies with all tax regulations while minimizing risks and penalties. Understanding the difference between cash and accrual accounting is essential for choosing the right method for your business. For small businesses, having a solid accounting system can make all the difference. It ensures you use your resources wisely and spot potential problems early, giving you a better chance to grow and succeed. After the adjusting entries are prepared, an adjusted trial balance is made. This is, essentially, a second round of trial balance reports which are used to test if the debits and credits are equal after the adjusting entries.

Recording Financial Transaction

Proper accounting allows a company’s management to better understand the financials of its business. This is so they can strategically plan its future expenditures in order to maximize profit. This method records income and expenses when they are earned or incurred, regardless of cash flow. While more complex, accrual accounting provides a clearer picture of a business’s financial position, especially for companies with long-term contracts or credit transactions. It helps in better financial planning and is often preferred by larger businesses.

• This guide explores how to create a solid budget, track expenses, manage cash flow, and set financial goals.
• It’s also worth noting that while all CPAs are accountants, not all accountants are CPAs.
• The main goal of business accounting is to stay on top of important things like cash flow, expenses, and inventory.
• For many small businesses, Bench was an essential part of managing taxes and ensuring compliance with local, state, and federal regulations.
• On the other hand, managers use accounting reports to boost business efficiency and profitability.
• They relate specifically to the types of accounts listed above, and how transactions in these accounts are debited and credited.

How NOT to Use AI Systems in Financial Management

The payroll service automates payroll taxes, checks, and all year-end forms, but the accounting platform is mostly manual. While the tool is powerful and can help a skilled user navigate multiple aspects of running a business, it takes a good amount of know-how to get the most out of it. Refunds are often the result of miscalculated quarterly estimated tax payments. To calculate quarterly estimated tax payments accurately, you need to predict your income. It’s almost impossible to do so without reliable financial records produced through accurate accounting. It also shows all your bank account balances so you can reference both at the same time.

What is Trial Balance? Objectives, Preparation, Example, Limitations

Financial information should be presented in a simple and easy way so that the users i.e. investors, debenture holders, employees and government officials can understand it easily. It should be simple enough even for a person who is not aware about the rules and terms used in accounting. Some explanatory notes should be given so as to make the information more understandable. As mentioned earlier, accounting information is used by different stakeholders, especially the management, to decide the future course of action for the organisation.

They can track expenses, generate reports, and even help with invoicing. It’s a simple way to see if your business is making money or if adjustments are needed. Whether it’s monthly or quarterly, this practice keeps you informed and in control. Look at your current finances and imagine what you’ll need in the next few months or years. Budget for growth, plan for lean times, and always have a financial cushion.

Accounting Software to Simplify Your Tasks

There are additional styles that may appeal to certain businesses, like double entry accounting and accrual accounting, that some businesses may consider. Businesses have large groups of stakeholders who have a vested interest in the continued success of the enterprise. If a business, whether for-profit or nonprofit, becomes financially insolvent and can’t pay its bills, it will be forced to close.

How Do I Set up a Small Business Accounting System?

• These documents provide accurate wage reporting, along with Social Security and Medicare benefits.
• A skilled outsourced accounting team brings a wealth of experience that can help you navigate the complexities of financial reporting, tax filing, and compliance.
• Tax accounting requires specialized expertise and knowledge of tax codes and regulations.
• This is, essentially, a second round of trial balance reports which are used to test if the debits and credits are equal after the adjusting entries.
• To speed up action, you may hire accounting professionals or purchase accounting software to ensure accurate financial audits and reporting.
• Wolf has over 110 years of experience and the means to stabilize the financial operations of companies affected by the Bench Accounting closure.

A skilled CPA will save you time by communicating your company’s financial state to you in clear language, while anticipating your financial needs. Credit accounting involves analyzing all of a What is Legal E-Billing company’s unpaid bills and liabilities to make sure that a company’s cash isn’t constantly tied up in paying for them. Learn how to build, read, and use financial statements for your business so you can make more informed decisions. Bench simplifies your small business accounting by combining intuitive software that automates the busywork with real, professional human support.

Zoho Books

It’s the perfect report to review to make sure you have the cash available to tend to your debts and plan future payments. When a customer owes you money, it appears as Accounts Receivable (AR) on your balance sheet, which is generated automatically by your accounting software or manually by you or your accountant. On a cash basis, you only record transactions when money changes hands. If you receive an invoice on the 10th but don’t pay it until the 15th, the transaction is recorded on the 15th. At ground level, keeping track of all your tax information reporting is trickier than it sounds.

In accounting, only those transactions and events are recorded which can be measured in terms of money. At the end of the accounting period, the accountant must prepare the adjusting entries to update the accounts that are summarized in the financial statements. Business transactions are recorded in a journal (also known as Books of Original Entry) in a chronological order using the double-entry bookkeeping system. Understanding these terms is key to making sense of financial statements and making smart decisions for your business. Once you know what these concepts mean, it’s much easier to manage your money and plan for a successful future.

We’ve written a handy blog post that explores the key differences between invoice factoring and invoice discounting. There are resemblances between invoice financing and short-term credit facilities. In its core structure, invoice financing is anchored to a specific invoice or a set of receivables. This invoice acts as security, prompting the finance entity to provide the invoice-owning business with a cash advance. In exchange for this advance, businesses remit a portion of the invoice value to the financier as a service charge. It’s important to remember, however, that invoice financing can be expensive, especially when your customers are late to pay.

Pro #1: Quick cash access

You finance the invoice with a lender and receive 80%, or $40,000, upfront. Be prepared to provide detailed documentation about your business and accounts receivable, and communicate openly with the financing provider to address any questions or concerns. Continue managing your accounts receivable and working with the financing http://4dw.net/amazonia/part10.php provider to ensure a smooth process for all parties involved. Kay’s Catering hosted a corporate event for their client, Mega Software Solutions, and sent an invoice for $20,000 with a 30-day payment term. Invoice financing services can save your business in a pinch because you can access working capital quickly.

• While each lender’s risk criteria is unique, there are certain things they’ll be looking for.
• The factoring company then becomes responsible for collecting from your customers, making it an attractive option for businesses that don’t want to chase down unpaid invoices.
• This percentage can vary but often falls between 70–90% for accounts receivable and 50–70% for inventory.
• Compare your top small business financing options, from over 160 financial products – with Nav.
• The trade credit insurer defines a credit limit for each customer corresponding to the maximum recommended trading amount.

The Complete Guide To Getting A Free Square Card Reader For Your Business

Invoice financing can provide funds that businesses can use immediately for working capital, payroll, supplier payment, expanding operations, investment, or other necessary payments. When your customer pays the invoice, you receive the remaining 15%, minus the lender’s fees. Typically, you’ll be charged a processing fee (about 3%), as well as a factor fee. The factor fee, usually about 1% to 2%, is charged on the total value of the invoice for each week it takes the customer to pay.

Is Invoice Financing Appropriate for Small Businesses?

Generally, invoice financing companies will focus on the quality of your invoices, as well as your customers’ repayment history, when determining whether or not you qualify for financing. SME invoice financing is one of the non-banking funding sources which are filling the need for capital for smaller businesses or new businesses without a long track record. As with invoice factoring, a factor rate is used with a merchant cash advance instead of an interest rate. Another similarity is that your number of sales, rather than your credit history, is the most important factor in qualifying for a merchant cash advance.

However, it’s important to weigh your options, clientele, and future financial goals carefully. Then, you choose a reputable provider and move forward with the cash advancement process. With invoice factoring, the invoice factoring company takes responsibility for collecting http://astrolab.ru/cgi-bin/dw.cgi-type=pr&dl=63&page=3.html payment from your customer, not you. Instead, the invoice factoring company will likely charge a factoring fee to your B2C client, which is a percentage of the invoice amount. Next, you’ll submit a copy of the $5,000 unpaid invoice to an invoice factoring company.

• As customers pay their outstanding invoices, the business uses those funds to repay the loan.
• We do not include the universe of companies or financial offers that may be available to you.
• This lender usually fronts the company between 70% and 85% of the total value of these invoices.
• Clean energy offers companies opportunities but also presents risks, which can be mitigated with trade credit insurance and surety bonds.
• Upon receipt of payment, the business settles the initial advanced sum with the financing entity, coupled with an interest fee, contingent on the duration the fund was utilized.
• You can use Funding Options to compare invoice finance products and find the best finance solutions on the market.

This would result in a difficult and expensive collections process involving both the bank and the business doing invoice financing with the bank. For businesses dealing with late payments and large invoices, invoice financing is a great option to ensure they get the money needed to maintain a healthy cash flow and uninterrupted growth. Typically, an invoice financing firm hands over 80-95% of your invoice https://catalogmineralov.ru/article/534.html amount. This gives you both immediate access to cash and more control over business decisions, as you no longer need to wait for clients to settle their due payments. Invoice financing rates can vary significantly depending on the provider, your business’s risk profile, and the terms of the agreement. Typically, providers charge fees based on the total invoice value or a percentage of the amount financed.

• Invoice financing and invoice factoring let you use unpaid invoices to generate quick cash, making them useful if your working capital is low as you wait for more money.
• Unfortunately, these options can be predatory (e.g. lenders that charge triple digit interest) and put your business into a financial hole that’s difficult to climb out of.
• Let’s look at a real-life example of when a small business owner might use invoice financing.
• Fortnox is a cloud-based accounting software platform based in Sweden that helps businesses manage their accounting and bookkeeping processes, as well as other financial admin like spend management.

Get the control and visibility your business needs

These companies assess the creditworthiness of the invoices and the businesses issuing them, determine the risk involved, and offer financing solutions tailored to the needs of different businesses. By offering timely access to working capital, invoice financing companies help businesses maintain operations, manage growth, seize opportunities, and avoid the pitfalls of late payments. Let’s say a small business provides goods or services to a client with invoice payment terms of net-30 days.

It’s used commonly in industries with long billing cycles, such as clothing, retail, manufacturing, etc. Confidentiality – particularly with invoice financing – keeps customers unaware that their invoices are being financed, which helps maintain trust and relationships. Now, here’s where things with invoice factoring start to differentiate themselves from the invoice financing process. Invoice financing is also referred to as accounts receivable financing or invoice discounting.

Invoice financing for small businesses with BILL

Invoice financing, receivables financing and invoice discounting, are terms often used interchangeably as they share many characteristics. Invoice financing is a collective term for other types of invoice-based lending provided in the market. Merchant Maverick’s ratings are editorial in nature, and are not aggregated from user reviews. Each staff reviewer at Merchant Maverick is a subject matter expert with experience researching, testing, and evaluating small business software and services. The rating of this company or service is based on the author’s expert opinion and analysis of the product, and assessed and seconded by another subject matter expert on staff before publication.

Lenders like AltLINE and Triumph Business Capital, on the other hand, offer invoice factoring. We believe everyone should be able to make financial decisions with confidence. What’s more, Juni is a comprehensive platform with features like invoice and card automation to help you manage your finances and streamline payment flows.

With invoice financing, lenders advance a percentage of your unpaid invoice amount — potentially as much as 90%. When your customer pays the invoice, you’ll pay the lender back the amount loaned plus fees and interest. New or small businesses might not qualify for traditional bank loans due to a lack of credit history or collateral. Invoice financing provides an alternative by leveraging outstanding invoices for capital. Even if they do, only clients with a good credit rating will be eligible for non-recourse. Additionally, non-recourse options may only be available under special conditions, such as when a client declares bankruptcy.

If your spouse is a nonresident alien, you can treat your spouse as a resident alien for tax purposes. If you choose this option, you can file a joint tax return with your spouse and have an increased Standard Deduction. You increase your Standard Deduction, but all your spouse’s worldwide income will be taxed by the United States. Married taxpayers generally must choose between Married Filing Jointly or Married Filing Separately, but taxpayers whose spouse is a nonresident alien may also file using the Head of Household status. Filing as Head of Household may give you benefits such as a greater potential refund. However, you must have another qualifying person to be eligible; your spouse doesn’t count.

Credits

• Same issue here, I already filed wrong and even got the Covid relief.
• As a legal U.S. resident, you’re subject to the same tax rules as U.S. citizens.
• Nonresidents of the U.S. are not liable to pay self-employment tax.
• If your spouse is not eligible for a Social Security number, they will need to apply for an Individual Taxpayer Identification Number (ITIN) from the IRS.

However, even if you don’t possess a green card, you are still considered a resident if you are physically present in the U.S. for at least 31 days in the current year and for a total of 183 days over the last three years. The problem is “resident” is not the same as “citizen” legally. So if your spouse is a citizen neither yes or  no is correct, because the answer is they’re a citizen. It’s also a problem that it asks even when you don’t indicate that they a resident (instead of a citizen) which is asked on one check box. Income exclusions generally have a greater impact for lowering your tax bill than tax credits because they can exclude all or part of your income from taxation. A tax treaty is a mutual agreement between two countries to resolve issues related to double taxation on income from each other’s respective citizens.

Do U.S. expats get tax refunds?

The threshold is much lower in certain cases such as with self-employment income. TurboTax cannot be used to file a nonresident tax return (form 1040 NR). All non-resident tax return forms like 1040NR or 8843, are available with instructions on the IRS website. You can also use software like Sprintax to guide you through the non-resident tax return preparation process. Citizenship and Immigration Service allows you to reside in the country legally, you are a resident alien.

The United States subjects your worldwide income to U.S. income tax, regardless of where you live. To make this easier, the Internal Revenue Code offers certain foreign income tax credits, tax deductions, and income exclusions, potentially reducing your U.S. tax bill each year. Additionally, U.S. citizens and resident aliens living outside the United States are generally allowed the same deductions as citizens and residents living in the United States. If you don’t have a green card and aren’t physically present in the U.S. for a sufficient number of days, you are considered a nonresident alien—but this doesn’t mean you are exempt from U.S. tax. As a non-resident, you must prepare a U.S. tax return on Form 1040NR or 1040NR-EZ. But unlike resident aliens, you only report the income you earn that comes from the U.S.

In the year of transition between being a nonresident and a resident for tax purposes, you are generally considered a Dual-Status Taxpayer and must file two tax returns for the year. If you are a nonresident of the U.S., you cannot claim the standard deduction. However, students and business apprentices from India may be eligible to claim the standard deduction under Article 21 of the U.S.A.-India Income Tax Treaty.

The IRS prefers e-filed returns because they offer more accuracy, avoid processing delays, and speed up refund delivery for taxpayers. Nonetheless, the remaining portion of taxpayers prefer to file taxes through the mail. If you choose the Married Filing Separately (MFS) filing status, you won’t treat your spouse as a resident for tax purposes, and therefore you won’t include your spouse’s income on your return.

• A nonresident who later becomes a resident alien in the same year (known as a dual status alien) will need to file a 1040 with a 1040-NR attachment.
• I am not sure if this is some weird AI thing, or what, but it has made me a bit uncomfortable with the reliability of using it this year.
• The IRS prefers e-filed returns because they offer more accuracy, avoid processing delays, and speed up refund delivery for taxpayers.
• Nonetheless, the remaining portion of taxpayers prefer to file taxes through the mail.
• However, when filing MFS, the Standard Deduction is less than Married Filing Jointly (MFJ), and you lose certain tax credits and benefits you would otherwise be eligible for.
• In the year of transition between being a nonresident and a resident for tax purposes, you are generally considered a Dual-Status Taxpayer.

Credits & Deductions

Income Tax Return for Certain Nonresident Aliens with No Dependents. We are thrilled to announce that Sprintax – the only online solution for nonresident federal and state tax returns – is now live for Federal E-Filing. This means that, by completing the easy Sprintax questionnaire, you can file your federal return directly with the IRS online.

Form 8889 can be attached to your form 1040 NR.  You would need to ask Sprintax if they do support the form. Because TurboTax does not support the 1040NR, you would not be able to file the form 8889 to file even though you need to use the form 8889. The following TurboTax Online offers may be available for tax year 2024. Intuit reserves the right to modify or terminate any offer at any time for any reason in its sole discretion. Unless otherwise stated, each can i use turbotax for non resident alien offer is not available in combination with any other TurboTax offers. Certain discount offers may not be valid for mobile in-app purchases and may be available only for a limited period of time.

Resident and nonresident aliens

Tax treaties typically determine how much tax each country can apply to a taxpayer’s income, but also to their capital, estate or wealth. If you want to qualify under the Physical Presence Test, you need to live outside the U.S. for a full 330 days during the tax year. A “full day” counts as 24 hours starting at midnight, and you need to be in the foreign country for every minute of those 24 hours. If you take advantage of the automatic 2-month extension, you should still try to pay any tax that is due by the original due date to avoid accruing interest on the outstanding balance.

Or, get unlimited help and advice from tax experts while you do your taxes with TurboTax Live Assisted. And if you want to file your own taxes, TurboTax will guide you step by step so you can feel confident they’ll be done right. No matter which way you file, we guarantee 100% accuracy and your maximum refund.Get started now by logging into TurboTax and file with confidence. Fortunately, when you file taxes online with H&R Block, our products support both nonresident and part-year resident taxes for several states. If an agreement exists between the two states, you will only need to pay to the home state.

This document, also popularly known as the sailing permit or departure permit, must be secured from the IRS before leaving the U.S. You will receive a sailing or departure permit after filing a Form 1040-C, U.S. If you cannot file your return by the due date, you should file Form 4868 to request an automatic extension of time to file. You must file Form 4868 by the regular due date of the return.

Find out more about how the IRS classifies resident aliens vs. non-resident aliens and how that affects the amount you owe in taxes. Just in time for the April 15th tax deadline, TurboTax is excited to announce a partnership with Sprintax.com to offer an easy and accurate online solution to help non-resident taxpayers prepare their own taxes. Sprintax.com, subsidiary of Taxback.com, is an online non-resident tax filing solution for international students.

Qualifying surviving spouse (QSS)

Same issue here, I already filed wrong and even got the Covid relief. If your spouse doesn’t have a Social Security number or ITIN, you’ll need to apply for one when you mail in your return.